Seite 1 von 1
Grafik - Kurven
Verfasst: 22.03.2021, 16:20
von bbock
Peano-Kurven gehören zu den raumfüllenden Kurven (sog. FASS-Kurven, space-
filling, self-
avoiding,
simple and self-
similar = raumfüllend, selbst-ausweichend, einfach und selbstähnlich). Das u.a. Programm wurde in Turbo Pascal geschrieben und zeichnet die Grafiken auf der Joyce.
- PEANO_1.0.zip
- PEANO Version 1.0
- (8.52 KiB) 3341-mal heruntergeladen
Re: Grafik - Kurven
Verfasst: 23.03.2021, 19:53
von bbock
Auch die Hilbert-Kurven gehören zu den FASS-Kurven; auch dieses Programm wurde in Turbo Pascal geschrieben:
Re: Grafik - Kurven
Verfasst: 13.04.2021, 21:51
von bbock
Die erste Version des Peano-Kurven-Programms hatte noch einen kleinen Skalierungsfehler. Dadurch wurde die unterste Linie nicht gezeichnet; das ist jetzt behoben.
Re: Grafik - Kurven
Verfasst: 14.06.2021, 21:17
von wnb
Auf Wunsch von Thomas nun auch ein Screenshot


Re: Grafik - Kurven
Verfasst: 23.11.2023, 00:41
von ein Thüringer
Mein Hirn hat kapituliert, aber Holger aus dem Robotrontechnik-Forum hat es geschafft, die Rekursion erst in Basic und dann auch in BasiCode zu programmieren, siehe 017 und 019 von
https://www.robotrontechnik.de/html/for ... fe904c82a0 .
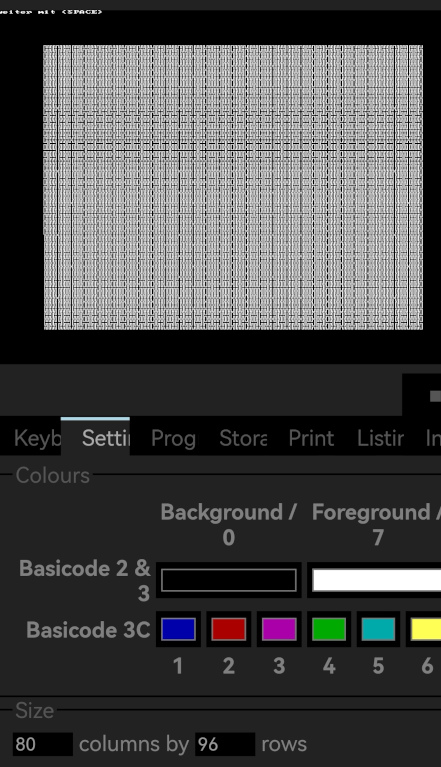
- Peanokurve in Verschachtelungstiefe 5 bei vergrößerter Zeilen- und Spaltenzahl im Online-Bascoder
- Smartphone.jpg (126.74 KiB) 52049 mal betrachtet
Code: Alles auswählen
1000 LET A=200:GOTO 20:REM Peano-Kurven
1001 REM https://de.wikipedia.org/wiki/Peano-Kurve
1010 REM go ...
1020 GOSUB 100
1022 PRINT "Peano Kurve"
1023 PRINT "Verschachtelungstiefe (0-5):"
1024 PRINT " (0 - Ende)"
1025 GOSUB 210
1026 IF IN < 49 THEN 950
1027 IF IN > 53 THEN 1020
1028 LET T=IN-48
1029 REM N - Rekursions-/ Verschachtelungstiefe
1030 LET N=T
1031 LET TR=0
1032 LET TS = 0.8/(3^T-1)
1034 GOSUB 600
1035 LET HO=0.1
1036 LET VE=0.9
1037 LET CN=1:GOSUB 620
1038 LET CN=0
1049 REM Hier beginnt die Arbeit
1050 GOSUB 1100
1060 LET HO=0:LET VE=0:LET CN=1
1061 GOSUB 620
1062 LET CN=0
1063 LET SR$="weiter mit <SPACE>"
1064 GOSUB 650
1065 GOSUB 210
1066 IF IN<> 32 THEN 1065
1069 GOTO 1020
1100 REM P -> PFQFP-F- SFRFS+F+ PFQFP
1102 IF N=0 THEN 1199
1103 LET N=N-1
1120 GOSUB 1100 :REM P
1121 GOSUB 10030 :REM F
1122 GOSUB 1200 :REM Q
1123 GOSUB 10030 :REM F
1124 GOSUB 1100 :REM P
1125 GOSUB 10020 :REM -
1126 GOSUB 10030 :REM F
1127 GOSUB 10020 :REM -
1128 GOSUB 1400 :REM S
1129 GOSUB 10030 :REM F
1130 GOSUB 1300 :REM R
1131 GOSUB 10030 :REM F
1132 GOSUB 1400 :REM S
1133 GOSUB 10010 :REM +
1134 GOSUB 10030 :REM F
1135 GOSUB 10010 :REM +
1136 GOSUB 1100 :REM P
1137 GOSUB 10030 :REM F
1138 GOSUB 1200 :REM Q
1139 GOSUB 10030 :REM F
1140 GOSUB 1100 :REM P
1190 LET N=N+1
1199 RETURN
1200 REM Q -> QFPFQ+F+ RFSFR-F- QFPFQ
1202 IF N=0 THEN 1299
1203 LET N=N-1
1220 GOSUB 1200 :REM Q
1221 GOSUB 10030 :REM F
1222 GOSUB 1100 :REM P
1223 GOSUB 10030 :REM F
1224 GOSUB 1200 :REM Q
1225 GOSUB 10010 :REM +
1226 GOSUB 10030 :REM F
1227 GOSUB 10010 :REM +
1228 GOSUB 1300 :REM R
1229 GOSUB 10030 :REM F
1230 GOSUB 1400 :REM S
1231 GOSUB 10030 :REM F
1232 GOSUB 1300 :REM R
1233 GOSUB 10020 :REM -
1234 GOSUB 10030 :REM F
1235 GOSUB 10020 :REM -
1236 GOSUB 1200 :REM Q
1237 GOSUB 10030 :REM F
1238 GOSUB 1100 :REM P
1239 GOSUB 10030 :REM F
1240 GOSUB 1200 :REM Q
1290 LET N=N+1
1299 RETURN
1300 REM R -> RFSFR-F- QFPFQ+F+ RFSFR
1302 IF N=0 THEN 1399
1303 LET N=N-1
1320 GOSUB 1300 :REM R
1321 GOSUB 10030 :REM F
1322 GOSUB 1400 :REM S
1323 GOSUB 10030 :REM F
1324 GOSUB 1300 :REM R
1325 GOSUB 10020 :REM -
1326 GOSUB 10030 :REM F
1327 GOSUB 10020 :REM -
1328 GOSUB 1200 :REM Q
1329 GOSUB 10030 :REM F
1330 GOSUB 1100 :REM P
1331 GOSUB 10030 :REM F
1332 GOSUB 1200 :REM Q
1333 GOSUB 10010 :REM +
1334 GOSUB 10030 :REM F
1335 GOSUB 10010 :REM +
1336 GOSUB 1300 :REM R
1337 GOSUB 10030 :REM F
1338 GOSUB 1400 :REM S
1339 GOSUB 10030 :REM F
1340 GOSUB 1300 :REM R
1390 LET N=N+1
1399 RETURN
1400 REM S -> SFRFS+F+ PFQFP-F- SFRFS
1402 IF N=0 THEN 1499
1403 LET N=N-1
1420 GOSUB 1400 :REM S
1421 GOSUB 10030 :REM F
1422 GOSUB 1300 :REM R
1423 GOSUB 10030 :REM F
1424 GOSUB 1400 :REM S
1425 GOSUB 10010 :REM +
1426 GOSUB 10030 :REM F
1427 GOSUB 10010 :REM +
1428 GOSUB 1100 :REM P
1429 GOSUB 10030 :REM F
1430 GOSUB 1200 :REM Q
1431 GOSUB 10030 :REM F
1432 GOSUB 1100 :REM P
1433 GOSUB 10020 :REM -
1434 GOSUB 10030 :REM F
1435 GOSUB 10020 :REM -
1436 GOSUB 1400 :REM S
1437 GOSUB 10030 :REM F
1438 GOSUB 1300 :REM R
1439 GOSUB 10030 :REM F
1440 GOSUB 1400 :REM S
1490 LET N=N+1
1499 RETURN
10000 REM TR - Turtle Richtung
10001 REM 0-Up 1-Left 2-Down 3-Right
10002 REM TS - Turtle Schrittweite
10010 REM Turtle Left (+)
10011 LET TR = TR+1
10012 IF TR > 3 THEN LET TR = 0
10013 RETURN
10020 REM Turtle Right (-)
10021 LET TR = TR-1
10022 IF TR < 0 THEN LET TR = 3
10023 RETURN
10030 REM Turtle Forward (F)
10032 IF TR=0 THEN LET VE=VE-TS:GOTO10037
10033 IF TR=1 THEN LET HO=HO-TS:GOTO10037
10034 IF TR=2 THEN LET VE=VE+TS:GOTO10037
10035 IF TR=3 THEN LET HO=HO+TS:GOTO10037
10037 GOSUB 630
10039 RETURN
Grafik - Kurven
Verfasst: 01.06.2024, 19:24
von ein Thüringer
Bei meinen Versuchen diese verflixte Rekursion in meinen Schädel zu bekommen stieß ich auf der Website eines Mathematikers der Universität von Ljubljana (Slowenien) auf weitere raumfüllende Kurven.
Die Knuth-Kurve
Das Logo-Programm von dort passt auch auf unserer Joyce. Wie bei den meisten Grafik-Sachen ist das Tempo beschaulich, aber in der CP/M-Box gibt es ja die F11-Taste.
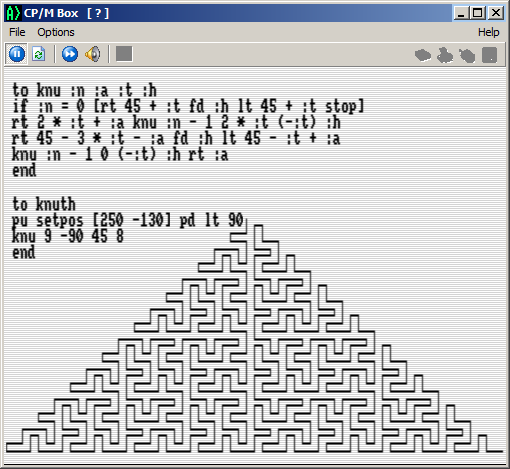
- Knuth.png (42.95 KiB) 50200 mal betrachtet
Die Wirth-Kurve
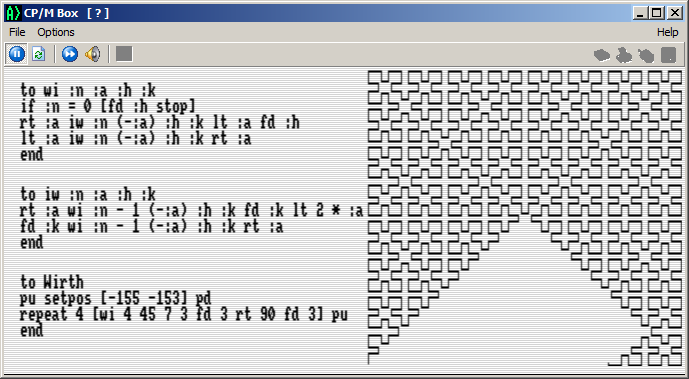
- Wirth.png (30.06 KiB) 50238 mal betrachtet
Die Sierpinski-Kurve
Hier musste erst die Berechnung der Quadratwurzel definiert werden - diese Funktion fehlt im Dr Logo des PCW.
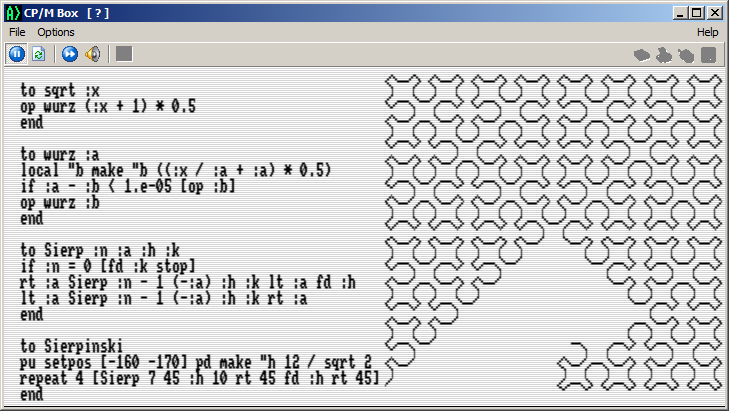
- Sierpins.png (37.75 KiB) 50238 mal betrachtet
